
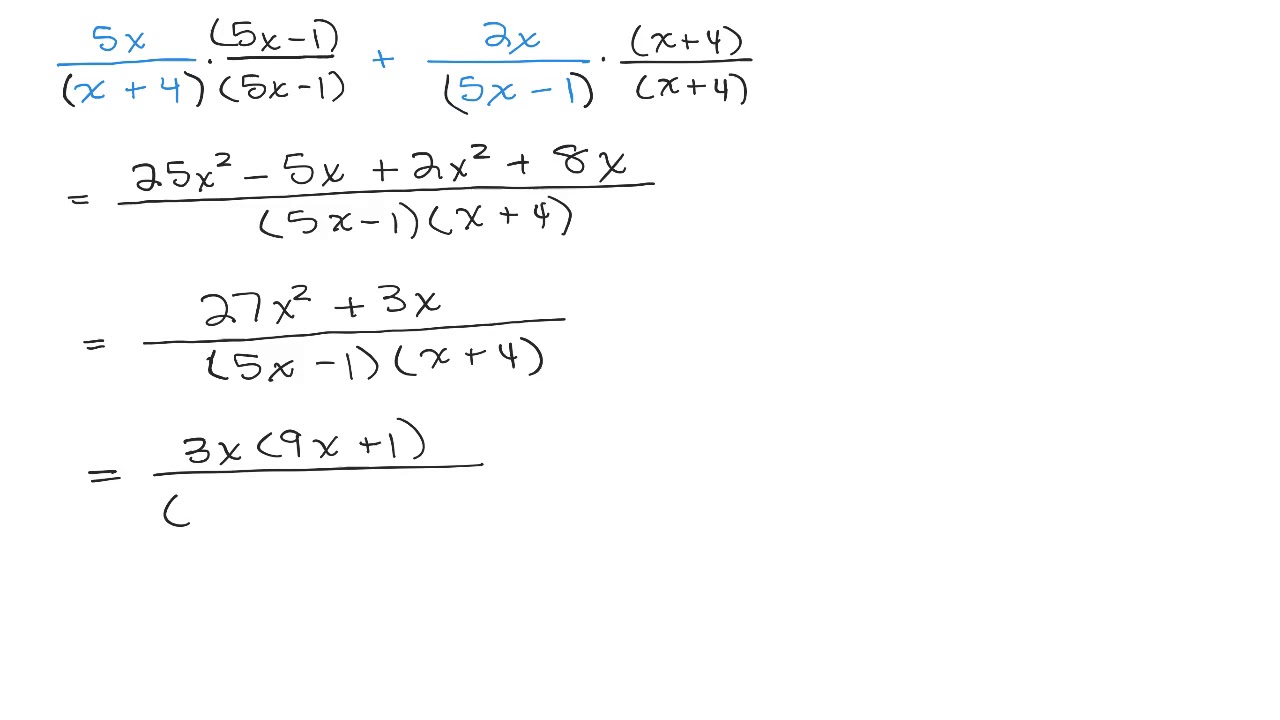
For example, integers can be factored into products of irreducible values called primes, while polynomials can be factored into products of irreducible polynomials.īut on an aesthetic level, doesn't it seem that both integers and polynomials lack a certain symmetry? Specifically, recall that they both have additive inverses, but not multiplicative ones.
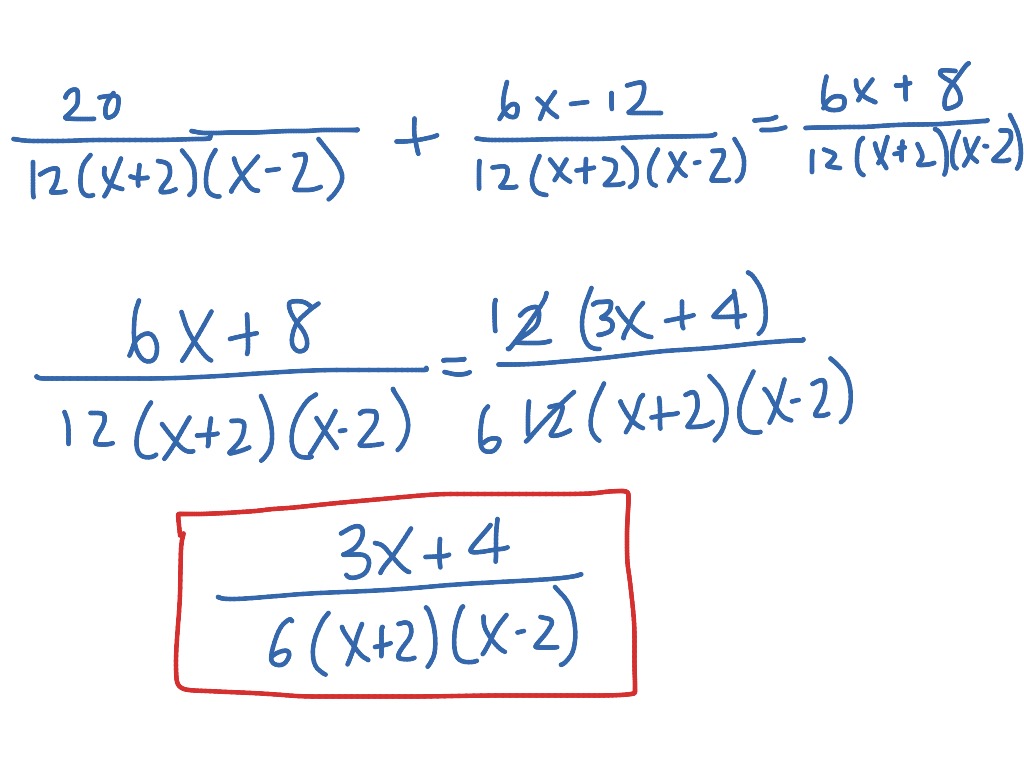
Note that they also share other commonalities. Further, their additions and multiplications are associative and commutative. Both are closed under addition, subtraction (which presumes additive inverses and an additive identity exists), and multiplication, but not division (noting that occasionally divisors go into dividends "evenly"). X out of the numerator but that's not going to cancel out with anything in the denominator and it looks like we are all done.As we have said before, the polynomials behave very much like integers. It doesn't seem like there's any easy way to simplify this further. We could add those two together to get a 27x² so we've already taken care of this, we've taken care, let meĭo it in that green color, so we've taken of this, we've taken care of those twoĪnd we're just left with a 5x, so + 5x and then all of that is over 2x-3 times 3x+1 3x+1 and we are and we are all done. It's a rational expression, and so let's see, we can look at, we can, our highest degree term here is the -8x³ so it's -8 - 8x³ and then we have a 15x² and we also have a 12x². 8x³ and then -4x² times -3 is 12x² and then our entire denominator our entire denominator we have a common denominator now so we were able to just add everything is 2x-3 2x-3 times 3x+1 times 3x+1 and let's see, how can we simplify this? So this is all going to be equal to, let me draw, make sure we recognize Everything you hated about adding fractions, youre gonna to hate worse with rational expressions.

So -4x² times 2x is -8x to the third power. Addition and subtraction are the hardest things youll be doing with rational expressions because, just like with regular fractions, youll have to convert these polynomial fractions to their lowest common denominators. The video you could see, try to figure out what Going to have 5x times 3x which is 15x² 5x times 1, which is + 5x, and then over here, let me do this in green, let's see, I could do -4x times 2x which would be -8x² and then -4x times -3 which is +12x². And so then I can rewriteĪll of this business as being equal to, well, in the numerator, in the numerator I'm Let me put parentheses around this so it doesn't look like Over here I have a denominator of 3x+1, I multiplied it by 2x-3, so I would take my numerator, which is -4x² and I would also multiply it by 2x-3. I multiplied it by 3x+1 over 3x+1, which is 1 as long asģx+1 does not equal zero. The numerator and denominator of a fraction may be. So the original numerator was 5x and now we're going to Rational expressions (fractions) can only be added or subtracted if they have a common denominator. So if we do that to the denominator, we don't want to change the value of the rational expression. Here the denominator to a (2x-3)(3x+1) we multiply the denominator by 3x+1. And so to go from 2x, to go from just a 2x-3
ADDING RATIONAL EXPRESSIONS PLUS
So we're going to make it 2x-3 times 3x+1 times 3x+1 and then plus plus something else over 2x-3 2x-3 times 3x+1. Let's make it let's make it 2x, I'm going to do this in another color. To be equal to something over our common denominator. We must do the same thing when adding or subtracting rational. So this is going to be equal to it's going to be equal to something let's see, it's going We have to rewrite the fractions so they share a common denominator before we are able to add. And so let's set up a common denominator. Both of these are aboutĪs factor as you can get and they don't share anything in common. The two denominators, especially in case like this where they don't seem Get a common denominator is you can just multiply You need to rewrite them so that you have a common denominator. Have different denominators and it's hard to add fractions when they have different denominators. So the first thing that you might have hit when you tried to do it, is you realized that they Okay, I'm assuming you've had a go at it. Video and try to add these two rational expressions.


 0 kommentar(er)
0 kommentar(er)
